Quantum computing for fluid dynamics and chemical reactions
Overview
Reacting flow is a system in which chemical reactions and fluid dynamics are tightly coupled. It includes combustion, plasmas, and nuclear reactions, and are critically important for energy conversion, materials engineering and many other industrial applications. However, their numerical analysis requires an extensive cost: the number of variables becomes enormous because many reacting species must be considered, and the coexistence of processes with small time scales (fast reactions) and large time scales (fluid motion, molecular diffusion, etc.) leads to computational stiffness.
As a new computing platform to overcome these challenges, we focus on quantum computers, which have been actively developed in recent years and are expected to become practical in the near future. Quantum computers are designed based on quantum mechanics and are expected to process certain classes of problems—such as linear algebra operations—at larger scales and higher speeds than conventional (classical) computers. Their operating principles are fundamentally different from those of classical computers, development of analysis methods tailored to quantum computation is requires. In our laboratory, we are studying approaches to accelerate the analysis of reactive-flow problems, including combustion, on quantum computers.
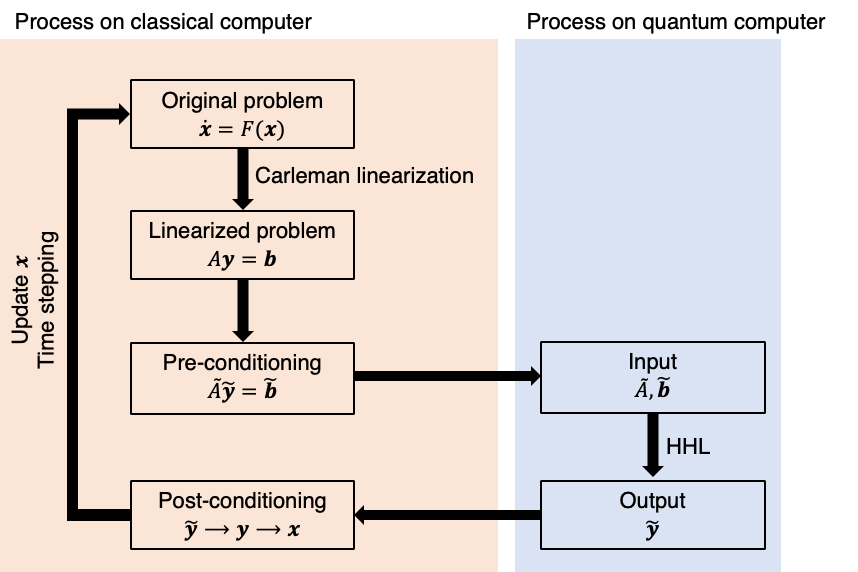
Schematic of possible quantum computing for non-liear dynamics
Recent Reports
Linearization shcemes for non-linear chemical reaction system
Chemical reactions are generally nonlinear, and thus cannot be directly cast into the linear-algebraic framework in which quantum computers excel. One of the most fundamental models for describing chemical kinetics is the Arrhenius rate law. For example, when one molecule each of species A and B react to produce species C, the reaction can be written as
A + B => C.
In this case, the reaction rate per unit time and unit volume, ω, is expressed as
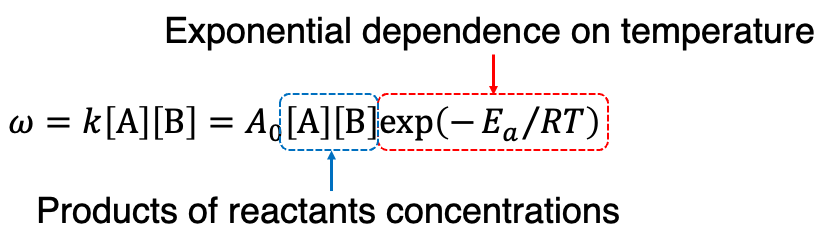
where A0, Ea, R, and T denote the pre-exponential factor, activation energy, gas constant, and temperature, respectively, and [X] represents the molar concentration of species X. This expression indicates that the reaction generally proceeds faster at higher reactant concentrations and higher temperatures. The equation also shows that chemical kinetics involves various nonlinearities, such as the product of concentrations ([A][B]) and the exponential dependence on temperature. Therefore, it is necessary to reformulate such nonlinear reaction models into linear problems which are more suitable for quantum computation.
In this study, we focus on a linearization method known as Carleman linearization. Carleman linearization introduces an augmented state vector whose components are nonlinear monomials, thereby representing a nonlinear system with polynomial nonlinearities as a (higher-dimensional) linear system. Although this augmentation increases the number of basis terms (variables), quantum computers may be able to handle many variables simultaneously, so the advantage of mapping nonlinear dynamics to a linear system while retaining the nonlinearity is expected to be significant.

To date, our laboratory has applied this approach to (i) combustion kinetics with the temperature fixed, thereby eliminating the exponential temperature dependence, and further extended it to (ii) combustion with temperature variations by approximating the temperature dependence via a Taylor expansion to obtain a polynomial form, which enables the application of Carleman linearization.

Validation of Carleman linearization for chemical reaction system of H2/Air mixture.

Validation of Carleman linearization for chemical reaction system of CH4/air ignition.
Emulation of quantum computers
Current quantum computers are still in a research phase, and two major challenges remain: their scale is not yet large enough, and they suffer from substantial noise. In contrast, applying quantum computation to large-scale, high-accuracy analyses such as reactive-flow simulations will ultimately require high-performance, large-scale quantum computers, but devices at that level do not yet exist.
To address this gap, we emulate quantum circuits on classical computers to perform noise-free simulations of quantum computations. This allows us to separate algorithm-induced accuracy limits and errors from those arising from hardware noise, making it possible to more clearly identify the causes of errors when running on real quantum devices.
In our laboratory, we have focused on quantum phase estimation (QPE), a core subroutine underlying many quantum algorithms, and developed an application that emulates QPE circuits efficiently and at high speed on GPUs.

Benchmark results for developed quantum phase estimation application.
Related publication
- Akiba, T., Morii, Y., Lee, M., Maruta, K., and Suzuki, Y., "Efficient evaluation of Arrhenius rates for quantum computing applications in reactive flow problems using Carleman linearization," Proceedings of the Combustion Institute 41, 105918 (2025).
- Akiba, T., and Morii, "GPU Benchmark through QPE Emulator with cuQuantum for Practical Quantum Applications," arXive:2507.17175 (2025).
Last update: Jan. 30th, 2026